欧几里得算法和裴蜀定理

发表于 更新于 分类于 阅读次数： 本文字数： 1.9k 阅读时长 ≈ 3 分钟
欧几里德算法（又称辗转相除法）和裴蜀定理在算法中的应用。

欧几里德算法（又称辗转相除法）和裴蜀定理在算法中的应用。

欧几里德算法

欧几里德算法，又称辗转相除法。

假设有非零正整数 A、B，其中 A > B，将 A 减 B 记为 C，即 A - B = C。
最大公约数记为 GCD（greatest common divisor），例如 A、B 的最大公约数记为 GCD(A, B)。
求证：GCD(A, B) = GCD(B, R),（其中 R 为 A 除以 B 的余数，或记为 R = A - n * B，n 为 A 除以 B 的商。即 R = A % B）

第一步：证明 GCD(A, B) 能够整除 C

1.因为 GCD(A, B) 是 A 的公约数，存在整数 X，使得 X * GCD(A, B) = A；

2.因为 GCD(A, B) 是 B 的公约数，存在整数 Y，使得 Y * GCD(A, B) = B；

3.因为 A - B = C，即

X * GCD(A, B) - Y * GCD(A, B) = C

(X - Y) * GCD(A, B) = C

使用图片表示即：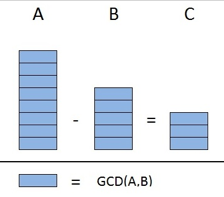

所以有结论：

GCD(A, B) 不仅是 A 和 B 的最大公约数，同时也是 C 的约数。

第二步：证明 GCD(B, C) 能够整除 A

1.因为 GCD(B, C) 是 B 的公约数，存在整数 M，使得 M * GCD(B, C) = B；

2.因为 GCD(B, C) 是 C 的公约数，存在整数 N，使得 N * GCD(B, C) = C；

3.因为 B + C = A，即

M * GCD(B, C) + N * GCD(B, C) = A

(M + N) * GCD(B, C) = A

使用图片表示即：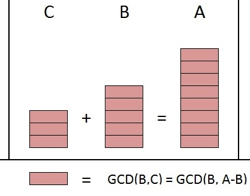

所以有结论：

GCD(B, C) 不仅是 B 和 C 的最大公约数，同时也是 A 的约数。

第三步：证明 GCD(A, B) = GCD(B, C)

1.因为 GCD(A, B) 是 A 和 B 的最大公约数，同时也是 C 的约数，所以 GCD(A, B) 一定也是 B 和 C 的约数。由于 GCD(B, C) 是 B 和 C 的最大公约数，所以存在

GCD(A, B) <= GCD(B, C)

2.因为 GCD(B, C) 是 B 和 C 的最大公约数，同时也是 A 的约数，所以 GCD(B, C) 一定也是 A 和 B 的约数。由于 GCD(A, B) 是 A 和 B 的最大公约数，所以存在

GCD(B, C) <= GCD(A, B)

3.由上可得 GCD(A, B) = GCD(B, C)

使用图片表示即：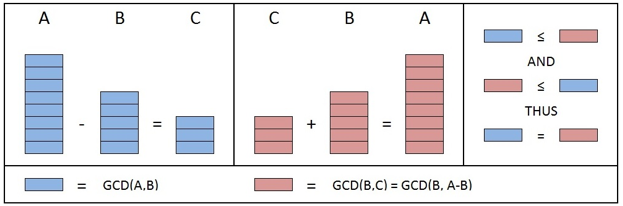

第四步：证明 GCD(A, B) = GCD(B, R)

1.因为 GCD(A, B) = GCD(B, C)，即 GCD(A, B) = GCD(B, A - B)

2.上式也可记为 GCD(A, B) = GCD(A - B, B)

3.重复上一步，即有

GCD(A, B) = GCD(A - B, B) = GCD(A - 2B, B) = … = GCD(A - n * B, B)

4.所以 GCD(A, B) = GCD(B, R)

欧几里得算法扩展，求最大公约数的算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public static int gcd(int a, int b) {
    if (a < 0 || b < 0) {
        return -1; // 数学上不考虑负数的约数
    }
    if (b == 0) {
        return a;
    }
    // 可以整除的时候才是约数，此时b的值就是最大公约数
    while (a % b != 0) {
        // 不停的取余
        int temp = a % b;
        a = b;
        b = temp;
    }
    return b;
}

裴蜀定理

对于不全为零的任意整数 a 和 b，记 g=gcd⁡(a,b)，其中 gcd⁡(a,b) 为 a 和 b 的最小公约数，则对于任意整数 x 和 y 都满足 ax+by是 g 的倍数，特别地，存在整数 x 和 y 满足 ax+by=g。

「裴蜀定理」也可以推广到多个整数的情况。对于不全为零的任意 n个整数 a1,a2,…an
，记这 n个数的最大公约数为 g，则对于任意 n 个整数 x1,x2,…xn都满足 ∑i=aixi
是 g 的倍数。一个重要的推论是：正整数 a1到 an 的最大公约数是 1 的充分必要条件是存在 n 个整数 x1到 xn满足 ∑i=aixi=1.

裴蜀定理扩展

1250. 检查「好数组

1
2
3
4
5
6
7
8
9
10
public boolean isGoodArray(int[] nums) {
        int divisor = nums[0];
        for (int num : nums) {
            divisor = gcd(divisor, num);
            if (divisor == 1) {
                break;
            }
        }
        return divisor == 1;
    }